4  Generic Identification in Linear Causal Models with OSCAR

Authors

Affiliations

Leopold Mareis

Technical University of Munich

Anthony Della Vecchia

TU Berlin

Bejamin Hollering

Max Planck Institute for Mathematics in the Sciences

Resource	Information
Git + DOI	Git Zenodo.18709429
Short Description	This notebook demonstrates the computational algebraic procedure in OSCAR to determine the identifiability of model parameters in linear graphical models.

4.1 Linear Structural Equation Models

Let \(\Lambda \in \mathbb{R}^{d\times d}\) be an upper-diagonal design matrix and let \(\varepsilon \sim P_\varepsilon\) be a centered random error vector with covariance matrix \(\Omega\). A random variable \(X\) is said to follow a linear model if it satisfies the structural equations \[ X = \Lambda^\top X + \varepsilon. \] The resulting covariance matrix \(\Sigma\) on a dataset \((X^{i})_{i \in [n]}\) defines the following system of equations: \[\Sigma := Cov(X) = (Id - \Lambda^\top)^{-T} \Omega (Id - \Lambda)^{-1} \] These equations specify algebraic relations via polynomials on the observed covariance matrix. They can be used to verify a proposed model class and to identify model parameters.

4.2 Acyclic Directed Mixed Graphs (ADMGs)

Let the four-variate random vector \(X\) follow the structural equations \[ \begin{pmatrix} X_1 \\ X_2 \\ X_3 \\ X_4 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \lambda_{12} & \lambda_{13} & 0 & 0 \\ 0 & 0 & \lambda_{34} & 0 \end{pmatrix} \begin{pmatrix} X_1 \\ X_2 \\ X_3 \\ X_4 \end{pmatrix} + \begin{pmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \varepsilon_4 \end{pmatrix} \quad , Cov(\varepsilon) = \begin{pmatrix} \omega_{11} & 0 & 0 & 0 \\ 0 & \omega_{22} & \omega_{23} & 0 \\ 0 & \omega_{23} & \omega_{33} &\omega_{34} \\ 0 & 0 & \omega_{34} & \omega_{44} \end{pmatrix}.\] This random vector satisfies Markov properties indicating (conditional) independencies with respect to the following graph:

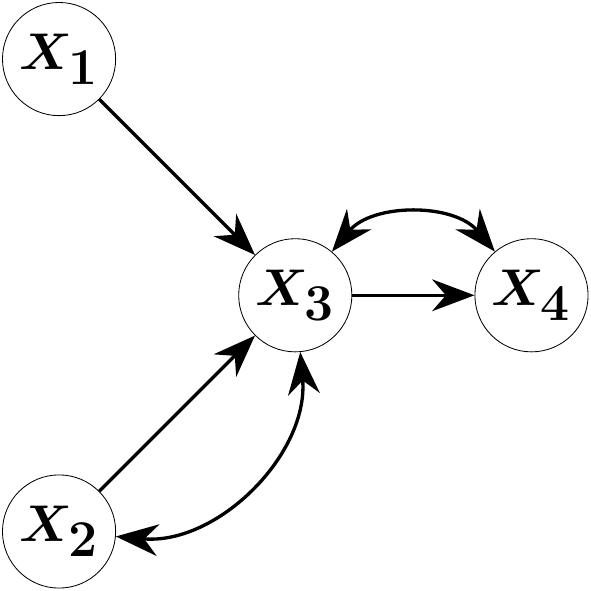
The direct effects \(\lambda_{21}\), \(\lambda_{31}\) and \(\lambda_{43}\) correspond to edges in the graph are parameters of interest. In practice, direct effects can for example model the effectiveness of a medical drug, the effectiveness of an institutional policy or of machine settings on the manufacturing quality. Experts or statistical structure learning can infer a potential graph inducing a structural model in which parameters are to be estimated.

There exists mathematical theory in the Half-Trek-Criterion on whether model parameters can be identified. This criterion is however sufficient but not necessary (Foygel, Draisma, and Drton (2012)). We show how computational algebra programs can be used to check parameter identifiability, closing the theoretical gap. All symbolic computations are performed in the Oscar Package embedded in Julia (“OSCAR – Open Source Computer Algebra Research System, Version 1.7.0” (2026)).

Foygel, Rina, Jan Draisma, and Mathias Drton. 2012. “Half-Trek Criterion for Generic Identifiability of Linear Structural Equation Models.” Ann. Statist. 40 (3): 1682–1713. https://doi.org/10.1214/12-AOS1012.

“OSCAR – Open Source Computer Algebra Research System, Version 1.7.0.” 2026. The OSCAR Team. https://www.oscar-system.org.

using Oscar

4.2.1 Computing the Model Variety

The polynomial equations induced by the covariance relations define an ideal, which is an algebraic null-set. This ideal consists of all model parameter configurations and covariance matrices that are aligned with the statistical model. A variety is a set of polynomial equations whose null-set is the ideal. Strategically reducing the variety and checking whether there exist a linear polynomial \[\lambda_{ij} g_1(\Sigma) - g_2(\Sigma)\] generically identifies the parameter \(\lambda_{ij}\) (Sullivant (2023), Proposition 16.1.8). Buchberger’s algorithm and variants for computing Groebner Basis eliminate the superflous model parameters after finite reductions. If the parameter is generically nonidentifiable, the finite reductions will return no such suitable polynomial. The following code chunk computes the variety for our ADMG example.

Sullivant, Seth. 2023. Algebraic Statistics. Vol. 194. American Mathematical Society.

function identify_parameters(M::GraphicalModel, 
                             return_elimination_ideal = false,
                             return_ideal = false)

  # get graph data from the model
  G = graph(M)
  if typeof(G) === Oscar.MixedGraph
    E = edges(G, Directed)
  else
    E = edges(G)
  end
  
  # get rings and parametrization
  S, s = model_ring(M)
  R, t = parameter_ring(M)
  phi = parametrization(M)
  
  # setup the elimination ideal
  elim_ring, elim_gens = polynomial_ring(coefficient_ring(R), vcat(symbols(R), symbols(S)))
  inject_R = hom(R, elim_ring, elim_gens[1:ngens(R)])
  inject_S = hom(S, elim_ring, elim_gens[ngens(R) + 1:ngens(elim_ring)])
  I = ideal([
    inject_S(s) * inject_R(denominator(phi(s))) - inject_R(numerator(phi(s))) for s in gens(S)
  ])
  if return_ideal
    return I
  end
  
  # eliminate
  out = Dict()
  for e in E
    l = t[e]
    other_params = [inject_R(i) for i in values(t) if i != l]
    J = eliminate(I, other_params)
    if return_elimination_ideal
      out[e] = J
    else
      out[e] = contains_linear_poly(J, inject_R(l), ngens(R))
    end
  end
  
  return out
end

function print_dictionary(out::Dict{Any, Any})
    for (i, edge) in enumerate(keys(out))
        println(edge)
        show(stdout, "text/plain", out[edge])
        println()
        if i < length(out)
            println()
        end
    end
end

directed_edges = [[1, 3], [2, 3], [3, 4]]
bidirected_edges = [[2, 3], [3, 4]]
graph_admg = graph_from_edges(Mixed, directed_edges, bidirected_edges)
model_admg = gaussian_graphical_model(graph_admg)

variety_admg = identify_parameters(model_admg, false, true)
display(variety_admg)

Ideal generated by
  -w[1] + s[1, 1]
  s[1, 2]
  -l[1, 3]*w[1] + s[1, 3]
  -l[1, 3]*l[3, 4]*w[1] + s[1, 4]
  -w[2] + s[2, 2]
  -l[2, 3]*w[2] - w[3, 2] + s[2, 3]
  -l[2, 3]*l[3, 4]*w[2] - l[3, 4]*w[3, 2] + s[2, 4]
  -l[1, 3]^2*w[1] - l[2, 3]^2*w[2] - 2*l[2, 3]*w[3, 2] - w[3] + s[3, 3]
  -l[1, 3]^2*l[3, 4]*w[1] - l[2, 3]^2*l[3, 4]*w[2] - 2*l[2, 3]*l[3, 4]*w[3, 2] - l[3, 4]*w[3] - w[4, 3] + s[3, 4]
  -l[1, 3]^2*l[3, 4]^2*w[1] - l[2, 3]^2*l[3, 4]^2*w[2] - 2*l[2, 3]*l[3, 4]^2*w[3, 2] - l[3, 4]^2*w[3] - 2*l[3, 4]*w[4, 3] - w[4] + s[4, 4]

The function identify_parameters creates a joint polynomial ring on the entries of \(\Lambda\) (l[i, j]), \(\Omega\) (w[i]) and \(\Sigma\) (s[i, j]). Note that we call the function gaussian_graphical_model although the error might be non-Gaussian. This is fine. It solely provides the necessary covariance relations after calling the method parametrization on the returned model. The variety is constructed from the polynomial relations \[(- (Id - \Lambda^\top)^{-T} \Omega (Id - \Lambda)^{-1})_{ij} - \Sigma_{ij} = 0 \quad \forall i,j \in [d]\] on the joint ring. The left-hand-side, as a potential rational function in the parameter ring, is handled though the numerator and denominator methods. The model generators are the \(\Sigma_{ij}\) entries s[i, j].

In our example, the second variety polynomial \(\sigma_{21}\) encodes that \(X_1\) and \(X_2\) are uncorrelated. This is the only visible requirement on the space of positive definite \(4\times 4\) matrices to be a correlation matrix of the proposed statistical model. In contrast, the first equation does identify the error variance \(Var(\varepsilon_1)\) as \(Var(X_1)\).

4.2.2 Computing the Elimination Ideal

The displayed variety above does not contain linear polynomial of the form \(\lambda g_1(\Sigma) - g_2(\Sigma)\) for \(\lambda \in \{\lambda_{13}, \lambda_{23}, \lambda_{34}\}\). It might however be possible to add or substract multiples of these polynomials to achieve such form. This procedure is implemented in the method eliminate by computing a Groebner basis and is carried out below.

elimination_admg = identify_parameters(model_admg, true)
print_dictionary(elimination_admg)

Edge(3, 4)
Ideal generated by
  s[1, 2]
  -s[1, 3]*s[2, 4] + s[1, 4]*s[2, 3]
  l[3, 4]*s[2, 3] - s[2, 4]
  l[3, 4]*s[1, 3] - s[1, 4]

Edge(1, 3)
Ideal generated by
  s[1, 2]
  -s[1, 3]*s[2, 4] + s[1, 4]*s[2, 3]
  l[1, 3]*s[1, 1] - s[1, 3]

Edge(2, 3)
Ideal generated by
  s[1, 2]
  -s[1, 3]*s[2, 4] + s[1, 4]*s[2, 3]

Inspecting the first variety indicates that there exists with \(-\sigma_{13}\sigma_{24} + \sigma_{14}\sigma_{23}\) a second requirement on the space of \(4\times 4\) covariance matrices. By the completeness of the Groebner basis, there can not exist any other requirement. The last two polynomials, \[ \begin{align} &\lambda_{34} \cdot \sigma_{23} - \sigma_{24} \\ &\lambda_{34} \cdot \sigma_{13} - \sigma_{14} \end{align} \] both identify the parameter \(\lambda_{34}\). In contrast, the parameter \(\lambda_{13}\) is generically nonidentifiable as there exists no suitable polynomial in the elimination variety. Statistically this is due to the overparameterization between \(X_2\) and \(X_3\) through the directed and bidirected edge. The method contains_linear_poly below finally filters all elimination variety polynomials for the required linear form which would imply generic parameter identifiablility. It returns one one of potentially many identification formulas.

function contains_linear_poly(J::MPolyIdeal, l::MPolyRingElem, nparams::Int)

  R = base_ring(J)
  
  for f in gens(J)
    exps = exponents(f)
    for v in exps
      # check for ideal generator with only one of its monomials containing 
      # l and with degree 1
      if v[var_index(l)] == 1 && sum(sum(e[1:nparams]) for e in exps) == 1
        return (true, f)
      end
    end
  end
  
  return (false, R(0))
end

identification_admg = identify_parameters(model_admg)
print_dictionary(identification_admg)

Edge(3, 4)
(true, l[3, 4]*s[2, 3] - s[2, 4])

Edge(1, 3)
(true, l[1, 3]*s[1, 1] - s[1, 3])

Edge(2, 3)
(false, 0)

As expected, we find the parameters \(\lambda_{34}\) and \(\lambda_{12}\) to be identified. The parameter \(\lambda_{23}\) is not identifiable from the data.

4.3 Directed Acyclic Graphs

The same methodology can be applied to graphical modelling with directed acyclic graphs (DAGs). Let the three-variate random vector \(X\) be Markov to the following graph:

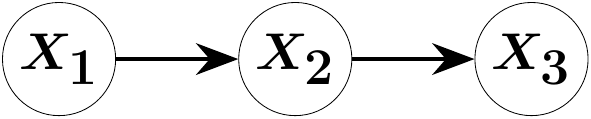
G = graph_from_edges(Directed, [[1, 2], [2, 3]])
M = gaussian_graphical_model(G)
out = identify_parameters(M)
print_dictionary(out)

Edge(1, 2)
(true, l[1, 2]*s[1, 1] - s[1, 2])

Edge(2, 3)
(true, l[2, 3]*s[2, 2] - s[2, 3])

Both linear parameters \(\lambda_{12}\) and \(\lambda_{23}\), corresponding to the edges \(X_1\rightarrow X_2\) and \(X_2\rightarrow X_3\), are identified.

4.4 Undirected Graphs

For undirected graphical modelling, assume the three-variate random vector \(X\) be Markov to the following graph:

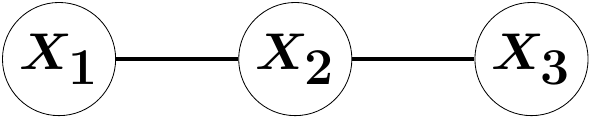
G = graph_from_edges(Undirected, [[1, 2], [2, 3]])
M = gaussian_graphical_model(G)
out = identify_parameters(M)
print_dictionary(out)

Edge(3, 2)
(false, 0)

Edge(2, 1)
(false, 0)

This model does not allow for any parameter identifiaction. The reason being that there exists a degree of freedom in scaling the precision matrix parameters \(K = \Sigma^{-1}\) that returns the same covariance matrix. One possibility to restrict the model class is through coloring (Boege et al. (2025)).

Boege, Tobias, Kaie Kubjas, Pratik Misra, and Liam Solus. 2025. “Coloured Gaussian Directed Acyclic Graphical Models.” Journal of the Royal Statistical Society Series B: Statistical Methodology, qkaf068.

4.4.1 Colored Undirected Graphs

Coloring graphs couples parameters. For example, we assume in the graph below that the error variance on all components is equal. This is indicated by the red coloring.

Computationally, coloring the graphs requires overloading the function parameter ring in Oscar (Boege et al. (2026)).

Boege, Tobias, Antony Della Vecchia, Marina Garrote-López, and Benjamin Hollering. 2026. “Algebraic Statistics in OSCAR.” arXiv Preprint arXiv:2601.15807.

import Oscar: parameter_ring, GraphDict, GraphMap

const ColoredGGM{Undirected} = GaussianGraphicalModel{
  Graph{Undirected}, @NamedTuple{color::GraphMap{Undirected}}
}

@attr Tuple{
  QQMPolyRing,
  GraphDict{QQMPolyRingElem}
} function parameter_ring(GM::ColoredGGM{Undirected})
  G = graph(GM)
  colors = unique([
    [G.color[e] for e in edges(G)]; [G.color[v] for v in vertices(G)]
  ])
  R, x = polynomial_ring(QQ, varnames(GM)[:k] => colors)
  color_dict = Dict{String, MPolyRingElem}(
    color => x[i] for (i, color) in enumerate(colors))

  gens_dict = GraphDict{QQMPolyRingElem}(
    Dict{Union{Int, Edge}, QQMPolyRingElem}(merge(
      Dict(e => color_dict[G.color[e]] for e in edges(G)),
      Dict(v => color_dict[G.color[v]] for v in vertices(G))
  )))
    
  return R, gens_dict
end

G = graph_from_labeled_edges(Dict((1, 2) => "2, 1", (2, 3) => "3, 2"),
                             Dict(1 => "red", 2 => "red", 3 => "red"); 
                             name=:color)
M = gaussian_graphical_model(G)
K = concentration_matrix(M)
show(stdout, "text/plain", K); println(); println()

out = identify_parameters(M)
print_dictionary(out)

[ k[red]   k[2, 1]         0]
[k[2, 1]    k[red]   k[3, 2]]
[      0   k[3, 2]    k[red]]

Edge(3, 2)
(false, 0)

Edge(2, 1)
(false, 0)

Both parameters, \(k_{21}\) and \(k_{32}\) are now identifiable.

4.5 Cyclic Graphs

The handling of cyclic graphs will be enabled in a future version of Oscar. Conceptually, this requires nothing new.